Up until now we have spoken only about primary shards, but we have another tool in our belt: replica shards. The main purpose of replicas is for failover, as discussed in Life Inside a Cluster: if the node holding a primary shard dies, a replica is promoted to the role of primary.
지금까지는 primary shard에 대해서만 이야기했다. 그러나 replica shard라는 또 다른 도구를 가지고 있다. Life Inside a Cluster에서 언급했지만, replica shard의 주요 목적은 장애에 대비하는 것이다. primary shard를 가진 node가 죽으면, replica가 primary의 역할을 하게 된다.
At index time, a replica shard does the same amount of work as the primary shard. New documents are first indexed on the primary and then on any replicas. Increasing the number of replicas does not change the capacity of the index.
색인 시에, replica shard는 primary shard와 동일한 양의 작업을 한다. 새로운 document는 먼저 primary에, 그 다음에 모든 replica에 색인된다. replica 수의 증가는 index의 용량을 변화시키지 않는다.
However, replica shards can serve read requests. If, as is often the case, your index is search heavy, you can increase search performance by increasing the number of replicas, but only if you also add extra hardware.
그러나, replica shard는 읽기 request를 처리할 수 있다. 대개의 경우와 마찬가지로, index가 검색에 부하가 많은 경우, replica의 수를 증가시켜 검색 성능을 향상시킬 수 있다. 그러나, 별도의 H/W를 추가 해야 한다.
Let’s return to our example of an index with two primary shards. We increased capacity of the index by adding a second node. Adding more nodes would not help us to add indexing capacity, but we could take advantage of the extra hardware at search time by increasing the number of replicas:
두 개의 primary shard를 가진 index의 예로 돌아가 보자. 두 번째 node를 추가하여 index의 용량을 증가시켰다. 더 많은 node를 추가하는 것은 색인 용량을 늘리는데 도움이 되지 않는다. 그러나, replica의 수를 늘려, 추가 H/W를 검색 시에 이용할 수 있다.
PUT /my_index/_settings { "number_of_replicas": 1 }
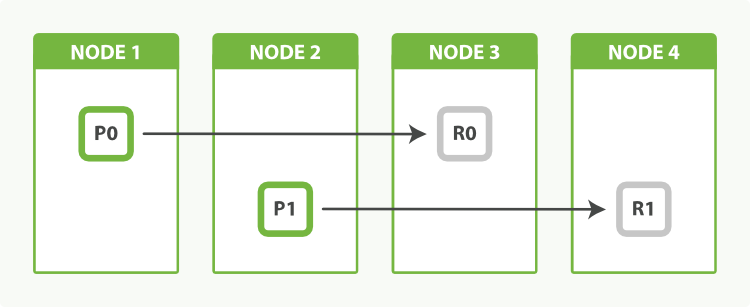
Having two primary shards, plus a replica of each primary, would give us a total of four shards: one for each node, as shown in Figure 51, “2개의 primary shard와 1개의 replica shard를 가진 index는 4개의 node로 수평 확장될 수 있다”.
두 개의 primary shard를 가지고 있고, 각각의 primary에 replica를 추가하면, Figure 51, “2개의 primary shard와 1개의 replica shard를 가진 index는 4개의 node로 수평 확장될 수 있다”에서 볼 수 있듯이, 각 node에 하나씩, 모두 4개의 shard를 가지게 된다.
Balancing Load with Replicasedit
Search performance depends on the response times of the slowest node, so it is a good idea to try to balance out the load across all nodes. If we added just one extra node instead of two, we would end up with two nodes having one shard each, and one node doing double the work with two shards.
검색 성능은 가장 느린 node의 response 시간에 달려 있다. 따라서, 모든 node에 대해, 부하의 균형을 맞추는 것이 좋다. 두 개가 아닌 하나의 별도 node를 추가 했다면, 각각 하나의 shard를 가진 두 개의 node를 가지게 되고, 하나의 node는 두 개의 shard를 가지고, 두 배의 작업을 하게 될 것이다.
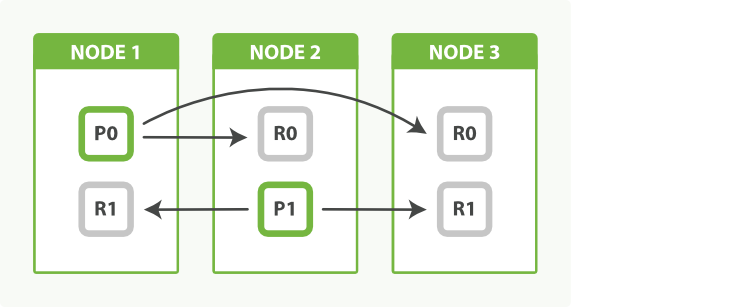
We can even things out by adjusting the number of replicas. By allocating two replicas instead of one, we end up with a total of six shards, which can be evenly divided between three nodes, as shown in Figure 52, “node 사이의 부하의 균형을 위해, replica의 수를 조정”:
replica의 수를 조정하여 해결할 수 있다. 하나가 아닌 두 개의 replica를 할당하면, 모두 6개의 shard를 가지게 되고, Figure 52, “node 사이의 부하의 균형을 위해, replica의 수를 조정”에서 볼 수 있듯이, 3개의 node로 공평하게 나누어질 수 있다.
PUT /my_index/_settings { "number_of_replicas": 2 }
As a bonus, we have also increased our availability. We can now afford to lose two nodes and still have a copy of all our data.
보너스로, 가용성 또한 향상되었다. 이제 2개의 node을 잃어도 된다. 그래도, 여전히 모든 데이터의 복사본을 가지고 있다.
The fact that node 3 holds two replicas and no primaries is not important. Replicas and primaries do the same amount of work; they just play slightly different roles. There is no need to ensure that primaries are distributed evenly across all nodes.
node 3이 primary 없이 2개의 replica를 가지고 있다는 사실은 중요하지 않다. replica와 primary는 동일한 양의 작업을 한다. 단지 약간 다른 역할을 할 뿐이다. primary가 모든 node에 공평하게 분산되어야 할 필요는 없다.
'2.X > 6. Modeling Your Data' 카테고리의 다른 글
| 6-4-03. Kagillion Shards (0) | 2017.09.23 |
|---|---|
| 6-4-04. Capacity Planning (0) | 2017.09.23 |
| 6-4-06. Multiple Indices (0) | 2017.09.23 |
| 6-4-07. Time-Based Data (0) | 2017.09.23 |
| 6-4-08. Index Templates (0) | 2017.09.23 |